了解 Swift 中的数值计算

WWDC20 Session 10217 - Explore numerical computing in Swift

Swift Numerics

Numerics 是一个 Apple 开源的 Swift 包，通过范型约束，提供更简单的方式，来使用所有标准库里的浮点型进行数值计算。

下面通过一个例子来看下这个包的作用。比如我们要在 Swift 中实现一个 Logit 模型的函数，在没有 Numerics 的情况下：

import Darwin
/// Logit 模型
///
/// https://en.wikipedia.org/wiki/Logit
///
/// - 参数 p:
///   取值范围 0...1。
///
/// - 返回值:
///   log(p/(1-p))。
func logit(_ p: Double) -> Double {
    log(p) - log1p(-p)
}

为了实现 log(p/(1-p))，我们需要调用 Darwin 里的 log 和 log1p，这两个函数位于 Darwin.C 中，是 C 标准库所定义的接口，里面用一系列同名函数来支持不同的具体浮点型。当我们用这类函数编写功能时，为了支持所有的浮点型（Double、Float、Float80 以及后续标准库可能增加的类型）就需要将重复的代码拷贝多次，大大提高了维护成本。

这时候可能你会想，要是能使用范型来代替这里面具体的浮点型就好了，这时候 Numerics 就派上用场了。

`Real` 协议

Numerics 里面提供了一个全新的 Real 协议，对这类计算的类型提供支持。通过 Real 协议，上面的例子可以改造成：

import Numerics

func logit<NumberType: Real>(_ p: NumberType) -> NumberType {
    .log(p) - .log(onePlus: -p)
}

给 NumberType 范型增加 Real 协议约束，并将 log 和 log1p 函数替换成 Numerics 里支持范型的 log 和 log(one plus:) 版本。所有浮点型都会遵循 Real 协议，这个改写后的 logit 函数，不仅能根据平台支持其对应的浮点型参数，在以后标准库增加新的浮点型时，也无需做额外的适配。

public protocol Real: FloatingPoint, RealFunctions, AlgebraicField {
}

Real 协议是一个协议组合，其中 FloatingPoint 协议是标准库中的协议，其余两个协议是 Numerics 里所提供的新协议。这里需要注意的是，对于开发者而言，只应该使用 Real 协议本身。

先来看看目前 Swift 标准库里已经存在关于数值的协议：

我们这里只关心其中关键的一部分：

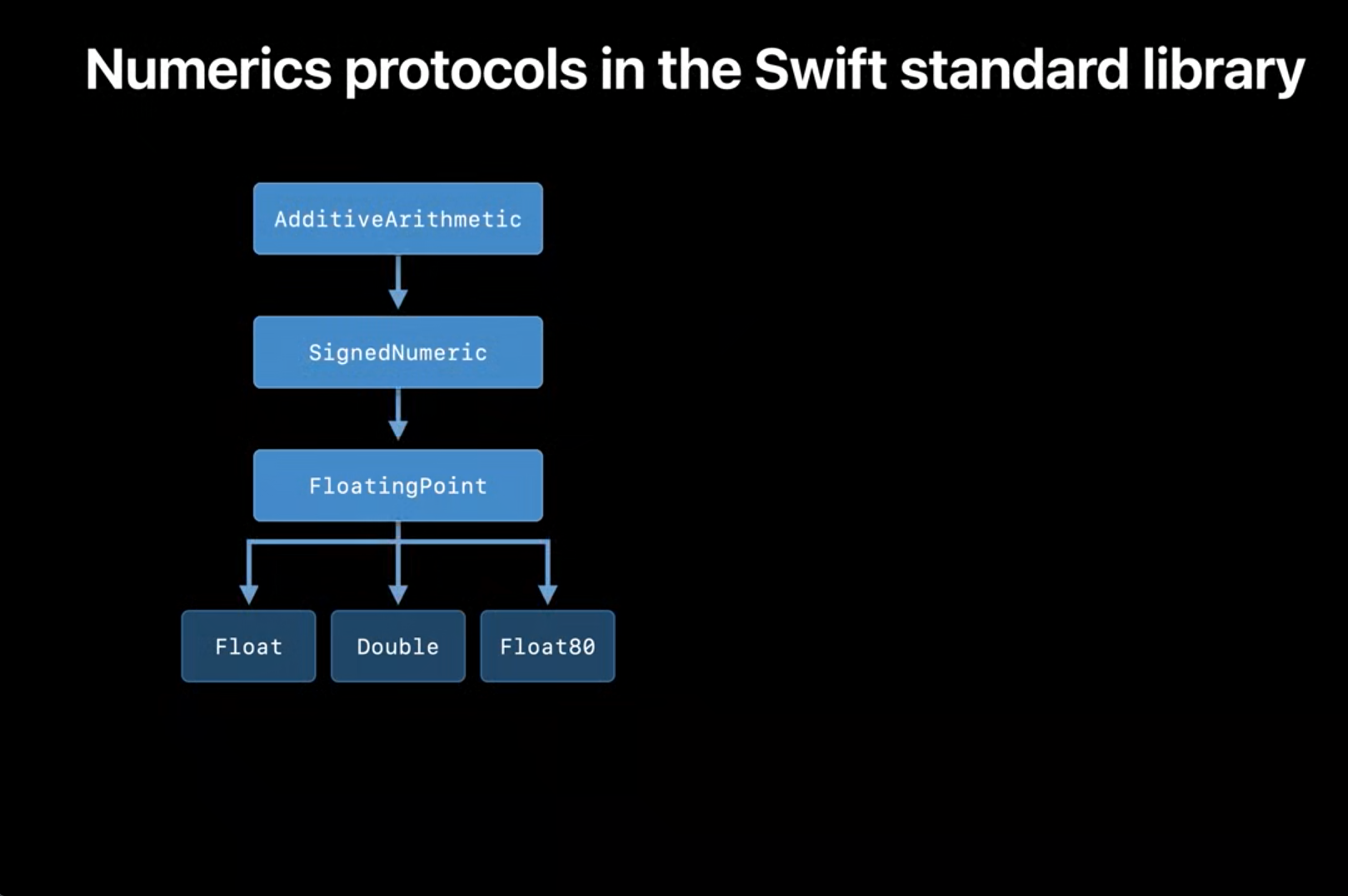
AdditiveArithmetic：用于支持加减法的类型，包括了大部分应该属于“数字”的概念，和数学领域的“代数群”几乎吻合。
SignedNumeric：拓展了乘法概念。
FloatingPoint：拓展了计算机中浮点型实现所需要的各种概念，比如比较、幂运算和有效位数等，还有各种常用的变量 infinity（∞）、nan 和 pi 等。

而 Numerics 是基于这些核心概念来构建的。

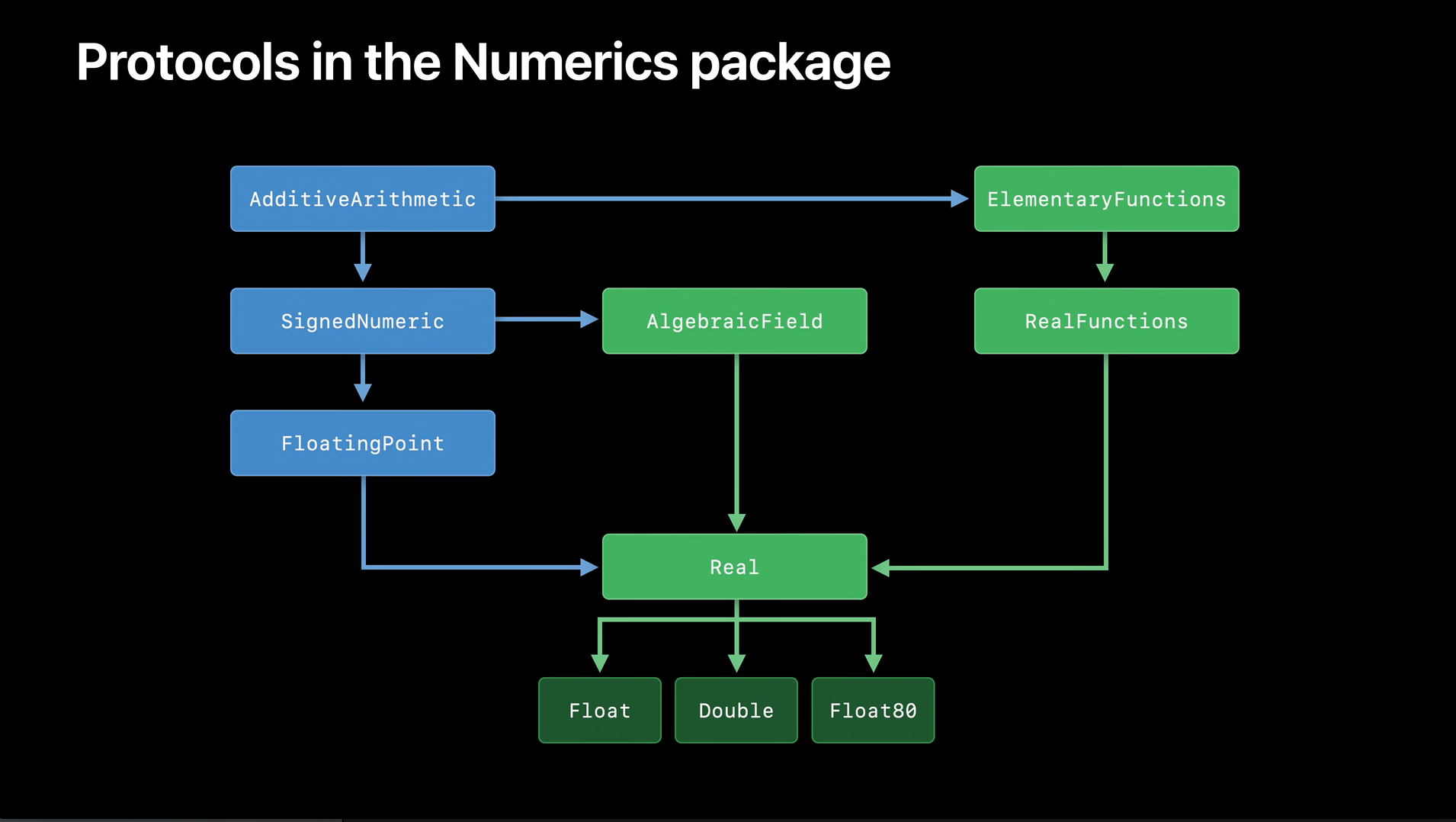
`AlgebraicField` 协议

public protocol AlgebraicField: SignedNumeric {
  static func /(a: Self, b: Self) -> Self
  
  /// 倒数
  var reciprocal: Self? { get }
  
  /// ...
}

在 SignedNumeric 的基础上拓展了除法概念。这样就支持了全部四则运算，数学领域称为”代数数域“，这也是这个协议名字的由来。

`ElementaryFunctions` 协议

public protocol ElementaryFunctions: AdditiveArithmetic {
  /// 指数
  static func exp(_ x: Self) -> Self
  
  /// exp(x) - 1
  static func expMinusOne(_ x: Self) -> Self
  
  /// 三角函数
  static func cos(_ x: Self) -> Self
  static func sin(_ x: Self) -> Self
  static func tan(_ x: Self) -> Self
  
  /// 对数
  static func log(_ x: Self) -> Self
  
	/// log(1 + x)
  static func log(onePlus x: Self) -> Self
  
  /// exp(y * log(x)) 
  static func pow(_ x: Self, _ y: Self) -> Self
  
  /// 幂
  static func pow(_ x: Self, _ n: Int) -> Self
  
  /// 次方根
  static func root(_ x: Self, _ n: Int) -> Self
  
  /// ...
}

在 AdditiveArithmetic 的基础上拓展了大量通用的浮点型函数，包括核心的三角函数、指数、对数、幂和次方根等。

`RealFunctions` 协议

public protocol RealFunctions: ElementaryFunctions {
  /// 误差函数
  static func erf(_ x: Self) -> Self

  /// sqrt(x*x + y*y)
  static func hypot(_ x: Self, _ y: Self) -> Self
  
  /// Γ(x)
  static func gamma(_ x: Self) -> Self
  
  /// log(|Γ(x)|)
  static func logGamma(_ x: Self) -> Self
  
  /// ...
}

在 ElementaryFuctions 的基础上拓展了更多类似但少用的函数，比如伽马函数、误差函数和更多底数的指数和对数等。

组合而成的 Real 协议因此巧妙地定义了标准浮点型所应该有的通用功能。这就是 Numerics 是如何将标准浮点型变得更加有用和优雅的。

虽然 Real 协议的概念很简单，但在实践中却格外强大。

范型支持
解决重复的代码
更低的维护成本
更好的兼容性（支持新的浮点型）

`Complex` 类型

Complex 类型是 Numerics 中的一部分，为 Swift 提供了复数支持，且是使用 Real 协议作为范型约束的。

import Numerics

let z = Complex(1.0, 2.0) // z = 1 + 2 i，这里默认是 Double

Complex 类型不仅本身很好用，同时也是一个使用 Real 协议进行范型数值编程的好范例。

/// 定义 NumberType 遵循 Real 协议
public struct Complex<NumberType> where NumberType: Real {
    /// 实数部分
    public var real: NumberType
  
    /// 虚数部分
    public var imaginary: NumberType
  
		/// ...
}

然后需要通过 SignedNumeric 协议支持基本运算函数。

extension Complex: SignedNumeric {
    public static func +(z: Complex, w: Complex) -> Complex {
        return Complex(z.real + w.real, z.imaginary + w.imaginary)
    }

    public static func -(z: Complex, w: Complex) -> Complex {
        return Complex(z.real - w.real, z.imaginary - w.imaginary)
    }

    public static func *(z: Complex, w: Complex) -> Complex {
        return Complex(z.real * w.real - z.imaginary * w.imaginary,
                       z.real * w.imaginary + z.imaginary * w.real)
    }
}

复数通常使用极坐标表示，所以需要定义长度和相位角。由于 Real 协议的帮助，我们很容易地计算这两个概念的值。同时还能得到一个便捷的构造函数。

extension Complex {
  	/// 长度
    public var length: NumberType {
        return .hypot(real, imaginary)
    }
  	
  	/// 相位角
    public var phase: NumberType {
        return .atan2(y: imaginary, x: real)
    }
  
    public init(length: NumberType, phase: NumberType) {
        self = Complex(.cos(phase), .sin(phase)).multiplied(by: length)
    }
}

Complex 类型是一个扁平的结构体，包含着两个浮点型的值。这样，和 C（_Complex double）与 C++ （std::complex<double>）里的复数类型有着精确匹配的内存布局。这使得 Swift 的复数和 C/C++ 有互操作的可能。在 Swift 中创建的复数缓冲区，可以通过指针传递给 C/C++ 的库使用。

来看这个使用 Accelerate 的 BLAS（线性代数计算标准）的例子：

import Numerics
import Accelerate

/// 100 个随机的复数
let z = (0 ..< 100).map {
    Complex(length: 1.0, phase: Double.random(in: -.pi ... .pi))
}

/// 计算 L2 范数（欧几里得范数）
let norm = cblas_dznrm2(z.count, &z, 1)

要注意的是，Swift 的 Comple 对待 ∞ 和 NaN 值和 C/C++ 不同，在桥接代码的时候需要小心。但 Swift 的处理更加简单和高效。这里有一个只包含复数乘除法的性能测试：

从图中可以看到，和 C 对比，乘法有 1.3x、除法有 3.8x，常数作为除数时的除法更有 10x 的速度提升。

同时，Numerics 还是一个持续维护的项目。

`Float16` 类型

Float16 是 Swift 标准库中新增的数据类型，顾名思义占用 16 位（2 字节）。

IEEE 754 标准格式
基于 ARM 的平台已经支持，包括 iOS、iPadOS、tvOS、watchOS
基于 x86 的平台正在支持中（和 Intel 在一起修复中）

Float16 是一个完整支持的标准浮点型。

遵循 BinaryFlatingPoint 和 SIMDScalar
遵循 Numerics 的 Real
支持所有的标准浮点型函数

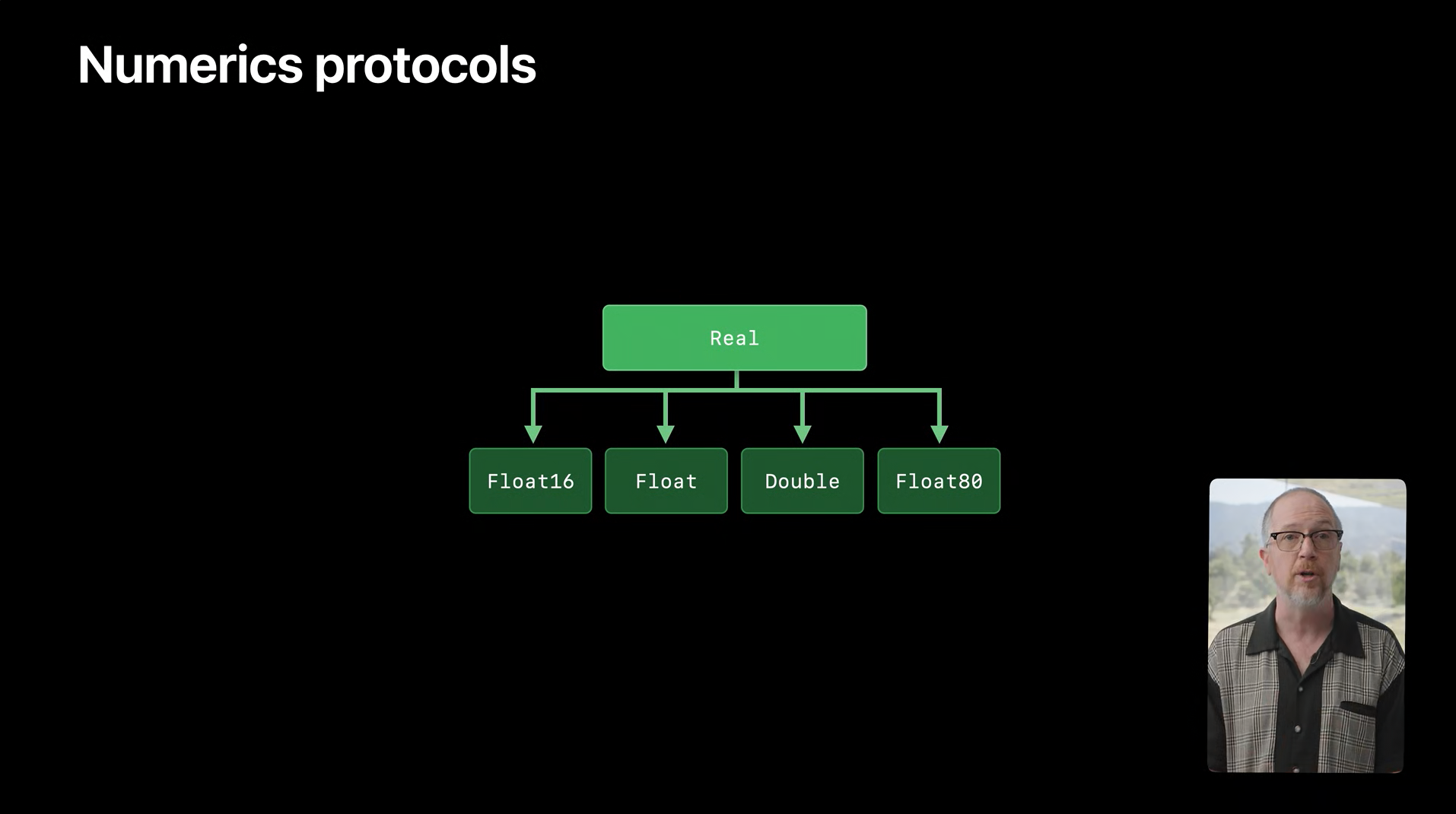
和其余数值类型一样，Float16 使用时也需要权衡利弊，这些得失大多仅和它的大小有关。

优点：

更好的性能
与 C/Objective-C 里 __fp16 类型的互操性

缺点：

低精度和小范围

在硬件支持上：

Apple GPU 已经支持（且为偏向选择）
Apple CPU 从 A11 Bionic 之后开始已经选择
- Scalar（标量）性能与 Float/Double 相同
- SIMD 性能 2x 于 Float
更老的 CPU 通过（用 Float 操作）模拟支持

这里有一个简单的 BNNS 卷积计算性能测试：

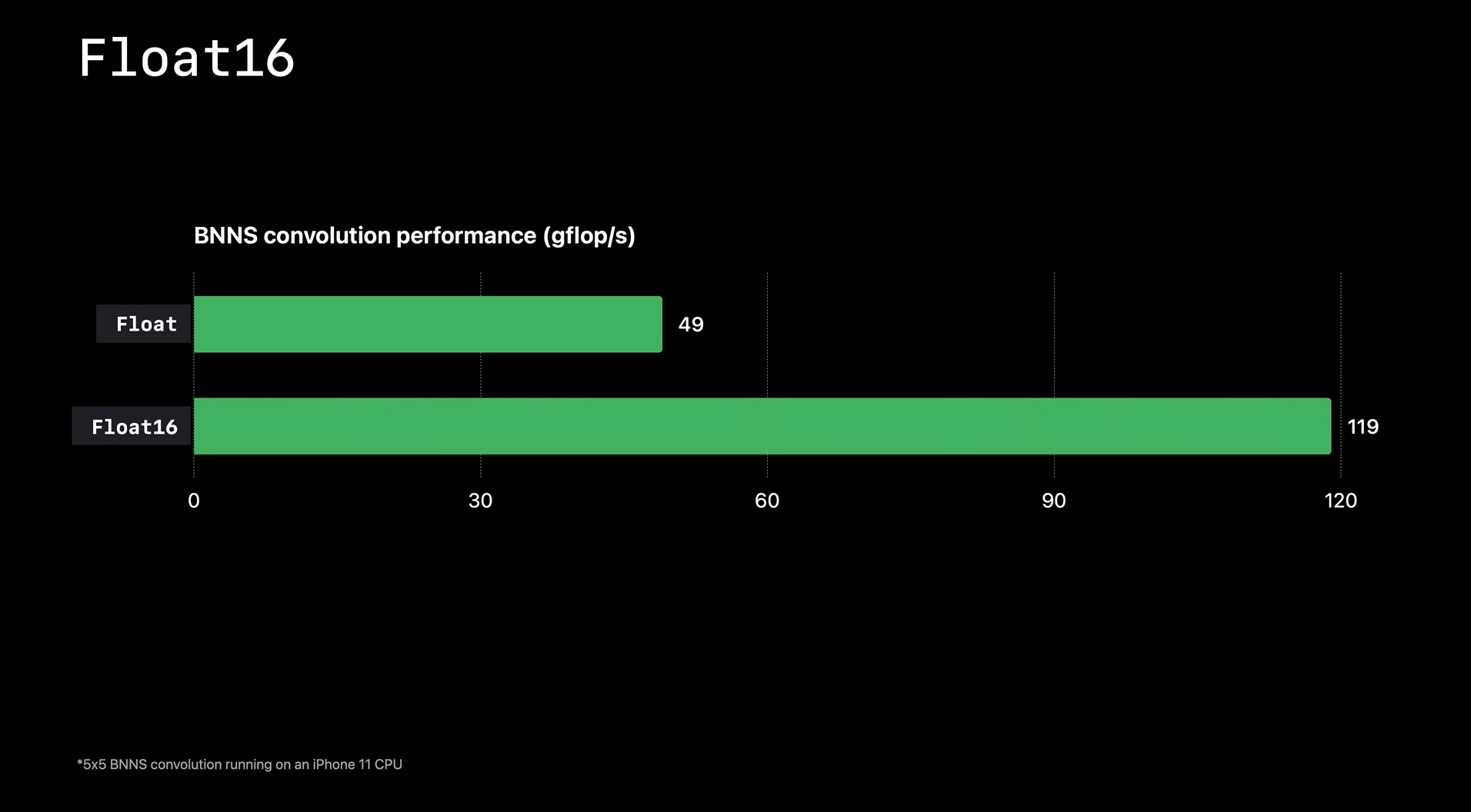
可以看到 Float16 的运算速度相对于 Float 有 2x 还多的提升。

最后

Float16 加入标准库，让 Swift 本身选择余地更多，可以踏足的领域更加丰富。

而 Swift Numerics 这个项目，和 Apple 对 Swift 的态度是高度一致的：

开源开放
多平台支持
性能出众
和 C 良好的互操性

同时，Numerics 作为 Apple 开源的 Swift 包，也是一个给开发者学习如何编写和封装更优雅 Swift 代码的范例。

可见未来 Swift Only 的包/框架会越来越多，Apple 每年都在告诉（国内大厂）开发者，Swift YES！

Swift Numerics

Real 协议

AlgebraicField 协议

ElementaryFunctions 协议

RealFunctions 协议

Complex 类型

Float16 类型

最后